Ricorre oggi il Pi Day, giornata mondiale dedicata al pi greco, una delle costanti più importanti e famose della matematica. Che si ritrova praticamente in ogni aspetto della vita quotidiana

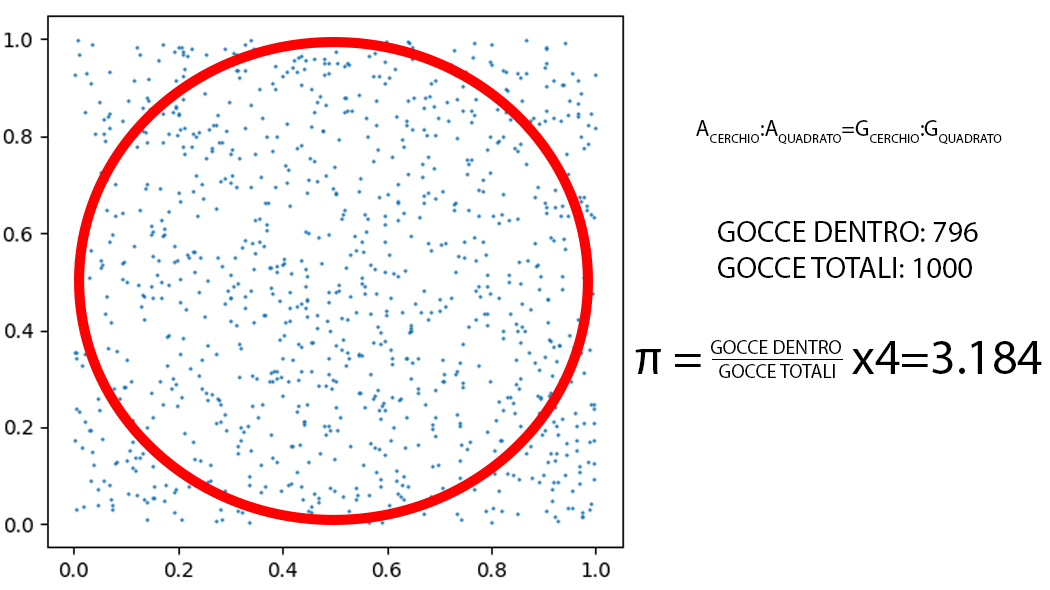
Prendete un cartoncino. Disegnateci un quadrato, poi iscrivetevi un cerchio. Poi mettete il cartoncino fuori dalla finestra e aspettate che piova. Infine, ritirate il cartoncino e contate le gocce di pioggia cadute nel cerchio e le gocce di pioggia cadute nel quadrato. Dividete i due numeri e moltiplicate il rapporto per quattro. Se avrete avuto abbastanza pazienza, aspettando la caduta di un numero sufficientemente alto di gocce, otterrete un numero molto vicino a 3,14. Non c’è niente di magico, naturalmente: il celeberrimo pi greco, la costante più famose della matematica, cui è dedicata la giornata di oggi (il Pi Day, che nella notazione americana si scrive per l’appunto 3/14), è praticamente ubiquo in natura e nel mondo che ci circonda, dal pallone che calciate in rete alla forma delle ali degli aerei, passando per l’iride dei vostri occhi e gli attorcigliamenti della doppia elica del dna. Ed è (anche) per questo che la comunità scientifica continua implacabile la propria caccia alle cifre decimali di pi greco – attualmente siamo arrivati a quota 5mila miliardi di numeri dopo la virgola – alla ricerca di regolarità, sequenze ripetute o altri segreti del numero.

Il pi greco è ubiquo, si diceva. Lo si può trovare, per esempio, addirittura guardando le stelle in cielo. Lo ha fatto Robert Matthews, della University of Aston in Birmingham, combinando un set di dati astronomici con la cosiddetta teoria dei numeri, una branca della matematica. In particolare, nella teoria dei numeri si postula (tra le altre cose) il fatto che per ogni insieme abbastanza grande di numeri casuali, la probabilità che due qualsiasi di essi non abbiano alcun fattore in comune (due numeri hanno un fattore in comune se sono divisibili per uno stesso numero che non sia 1) è pari al rapporto tra 6 e il quadrato di pi greco: Matthews ha calcolato le distanze angolari tra le 100 stelle più luminose del cielo e ha usato tali distanze per generare un milione di coppie di numeri casuali. Il 61% di esse non avevano fattori in comune, il che porta a una stima per pi greco di 3,12772, che si discosta di appena lo 0,4% dal valore reale.

La circonferenza di un cerchio con diametro unitario è pari a pi greco.

Ma non c’è bisogno di guardare al cielo. Il pi greco emerge serafico e imperturbabile come sempre anche dalle acque dei fiumi che solcano la superficie terrestre. Ad accorgersene è stato per primo il matematico Hans-Henrik Stolum, che in uno lavoro pubblicato su Science nel 1996 ha analizzato la sinuosità di fiumi e torrenti, scoprendo che questi scorrono secondo un processo di auto-organizzazione in una geometria frattale, caratterizzata dall’“alternanza di configurazioni ordinate e configurazioni caotiche”. In particolare, lo studio di Stolum ha evidenziato che il rapporto tra la lunghezza effettiva di un fiume dalla sorgente alla foce e la lunghezza in linea d’aria è approssimabile a pi greco. O, in altre parole, che la sinuosità media di un fiume è molto vicina a 3,14.

Il New Scientist ricorda che esiste persino un genere letterario ispirato a pi greco. Si chiama Pilish, ed è “uno stile di scrittura in cui la lunghezza delle parole consecutive è uguale alle cifre decimali di pi greco”. Un esempio? Questo poema di Joseph Shipley:

But a time I spent wandering in bloomy night;
Yon tower, tinkling chimewise, loftily opportune.
Out, up, and together came sudden to Sunday rite,
The one solemnly off to correct plenilune.

O, ancora, Cadaeimic Cadenza, di Mike Keith, un poema lungo ben 3835 parole. Keith è autore, tra l’altro, di un intero racconto in Pilish, della notevole lunghezza di ben 22 pagine.
Ancora affamati di pi greco? Potete rintracciarlo anche stando seduti nella vostra stanza, armati solo di un certo numero di stuzzicadenti e di un foglio bianco. Disegnate sul foglio delle righe bianche parallele, stando attenti a che la loro distanza sia maggiore della dimensione degli stuzzicadenti; lasciate quindi cadere gli stuzzicadenti stessi sul foglio, e misurate la percentuale di stuzzicadenti che interseca una linea. Se ne avete lasciati cadere abbastanza, tale percentuale sarà uguale alla lunghezza degli stuzzicadenti divisa per la distanza tra le linee e moltiplicata per due volte pi greco. Provare per credere.
Nella matematica e nella fisica, inutile dirlo, pi greco è praticamente ovunque. Compare all’interno di equazioni e formule fondamentali che non hanno niente a che vedere con geometria e circonferenze. Fa capolino nei moti ondosi, nel movimento dei pianeti, nelle collisioni tra le particelle elementari, nei modelli economici. Si trova persino nei calcoli relativi alla costruzione della piramide di Giza. E anche nel Vecchio Testamento, quando si descrivono le dimensioni del Tempio di Salomone, un passaggio fa riferimento implicito alla costante, approssimata (piuttosto rozzamente) a tre. Pi greco compare addirittura, racconta la Bbc, nelle trascrizioni del processo a O.J. Simpson, dove si può leggere una discussione tra il giudice e un agente federale a proposito del suo valore. Wislawa Szymborska, poetessa polacca premio Nobel per la letteratura, ha scritto una poesia su pi greco. La pop star Kate Bush ha cantato, nel suo album Aerial, le prime cento cifre del numero. E chi π ne ha, π ne metta.
FONTE

 

Pi greco Day, le 3+14 cose da sapere sul 3,14

Il 14 marzo torna il Pi greco Day. Ecco perché si chiama così e tante altre curiosità sul 3,14

Larry Shaw, un fisico dell’Exploratorium di San Francisco, e Jim Horton, matematico/musicista suo amico, stanno piacevolmente chiacchierando. È il 1983, è sera, qualche bicchiere, e la conversazione cade quasi subito sulla magnifica irrazionalità di Pi greco. Un numero, quel famoso 3,14 che non è solo il rapporto tra la circonferenza e il suo diametro, ma che costituisce una sorta di mistero multidimensionale. È lì che, per la prima volta, a Shaw viene l’idea di celebrare il Pi Greco Day.
Il 14 marzo 1988, chi si fosse trovato dalle parti di San Francisco avrebbe potuto vedere un piccolo gruppetto di persone, formate dallo staff dell’Exploratorium e da gente qualunque, che marciava solennemente intorno a un edificio (circolare, ça va sans dire) della struttura, per poi dirigersi voracemente verso delle crostate di frutta (“fruit PIes“) preparate per l’occasione. Era il primo Pi greco Day della storia. Da allora, la ricorrenza ha preso piede ovunque: partita dal mondo dei nerd, è arrivata fino al Congresso degli Stati Uniti, che nel 2009 ha istituito il National Pi Day.
Ovviamente il Pi greco, 3,14 per gli amici, si incarna nel 3/14, nella notazione giorno/mese, cioè il 14 marzo di ogni anno e oggi, ancora una volta, è il Pi greco Day. Si sa tanto di questa autentica icona della matematica: Pi greco è un numero irrazionale (ossia con infinite cifre decimali che non seguono nessuno schema ripetitivo) e contemporaneamente trascendente (cioè che non può venire fuori da un numero finito di operazioni numeriche). Infinite cifre non prevedibili. Oltre a dove trovare il Pi greco nella vita quotidiana e alle celebrazioni del Pi Day c’è tanto altro da dire su questo  instancabile numero, e sul modo in cui onorarlo degnamente.
1. Perché quello del 2015 è un Pi Day speciale?
Se l’anno scorso l’intero mese di marzo è stato salutato da qualcuno come “Il Mese del Pi”, a causa del fatto che si trattava di marzo (3) del 2014 (14), quest’anno la ricorrenza è ancora più speciale (ed è stato infatti chiamato da alcuni The Ultimate π Day). Il Pi greco, con le sue prime 9 cifre decimali, è infatti 3,141592653, e quindi c’è da cogliere l’attimo: in particolare quello che corrisponde alle 9:26:53 del 3/14/15, secondo la notazione americana. Data e tempo rappresenteranno le prime 10 cifre del Pi greco e, da qualche parte tra il secondo 53 e il secondo 54, verrà toccata la rappresentazione ESATTA di tutte le cifre del pi greco.
2. Quante cifre sono state calcolate finora?
Il record appartiene ad Alexander Yee e Shigeru Kondo, rispettivamente uno scienziato informatico americano e un
ingegnere di sistemi giapponese che alla fine del 2013, con la loro Pi-crunching machine, hanno raggiunto le 12 mila miliardi di cifre.
3. Qual è il record mondiale di cifre del Pi greco citate a memoria?
67.890, e appartiene al ventiquattrenne cinese Lu Chao, che lo ha stabilito il 20 novembre 2005. Per declamare questa poesia trascendente, ci ha messo 24 ore e 4 minuti e per impararla ha impiegato circa un anno. La 67891ma cifra era lo “0” e invece lui ha detto “5”. Peccato. Sembra che un giapponese di 69 anni, Akira Haraguchi, nel 2006 sia arrivato a 100mila cifre, ma il Guinness World Records non ha ancora omologato questo potenziale primato, e quindi il record resta di Chao.
4. Ogni giorno passiamo per Pi greco
Poiché Pi greco equivale a 3,141592653… ogni giorno potrebbe essere il Pi greco Day, o meglio, esiste un Pi greco
minute, ed è precisamente quello che corrisponde alle 3:14:15,92… Insomma, se amate tirare fino a tardi, sappiate che da qualche parte, tra le 3:14 e le tre e un quarto del mattino, state “toccando” il Pi greco minute.
5. Un numero, molti nomi
Il Pi greco è anche conosciuto come costante di Archimede, costante di Ludolph, costante Ludolphina, numero di
Ludolph. Se infatti fu Archimede, con il suo metodo di esaustione, a dare circa 2.500 anni fa la prima stima precisa di pi greco (arrivando alle prime due cifre), Ludolph van Ceulen, matematico tedesco del XVI secolo, spese la maggior parte della sua vita calcolando il valore di pi greco – usando essenzialmente i suoi stessi metodi. Riuscì ad arrivare a 35 cifre decimali e se le fece incidere sulla tomba.
6. Chi è riuscito a calcolare più cifre del Pi a mano?
Le 35 cifre calcolate a mano da Ludolph van Ceulen nel XVIII secolo e le 126 trovate dal matematico sloveno Jurij Vega nel XIX, impallidiscono di fronte alle 572 cifre calcolate a mano nel 1873 dal matematico dilettante inglese William Shanks. Shanks, che morì nel 1882, aveva l’hobby di calcolare costanti matematiche: ogni mattina, calcolava una nuova cifra, e passava poi il pomeriggio a controllare l’esattezza del risultato. Nel 1873 raggiunse le 707 cifre del Pi Greco, ma solo le prime 527 erano giuste.
7. La prima volta fu nel 1706
La prima volta che fu usato il Pi greco per rappresentare il rapporto tra la circonferenza di un cerchio e il suo diametro è nel lavoro di un matematico, William Jones, intitolato Synopsis Palmariorum Matheseos o New Introduction to the Mathematics. La lettera greca compare nella frase “1/2 Periphery (π)”, a proposito di un cerchio con raggio unitario, e Jones scelse proprio pi perché era la prima nella parola greca corrispondente a periphery. Successivamente, la lettera greca non fu più usata da nessuno a questo scopo, finché non comparve in Mechanica di Eulero, che era un big della matematica e che lanciò il Pi greco in tutto il mondo occidentale.
8. Prezzemolino
Quante sono le formule scientifiche in cui compare Pi greco? Ce ne sono un po’ in tutti i campi. Circonferenza, area del cerchio, volume della sfera, superficie della sfera, costante cosmologica, principio di indeterminazione di Heisenberg, equazione di campo della Relatività Generale di Einstein, legge di Coulomb per la forza elettrica, permeabilità magnetica dello spazio libero, periodo del pendolo, legge oraria del moto armonico semplice, identità di Eulero, flusso del campo gravitazionale, variazione del volume di una sbarra cilindrica soggetta a trazione, modulo della velocità nel moto circolare uniforme, legge di Stokes relativa alla forza di attrito viscoso, frazione continua di Ramanujan, funzione di probabilità della distribuzione normale (gaussiana), periodo di un pianeta (visto come una particella) in un campo centrale, etc.
9. Vi ricordate Second Life?
Il San Francisco Exploratorium anche quest’anno ha organizzato interessanti celebrazioni, tra cui una davvero nostalgica: quella sull’isola che l’Exploratorium ha in Second Life. Se esiste ancora qualcuno in quel mondo virtuale ormai praticamente abbandonato potrà visitare le mostre interattive organizzate su quest’isola.
10. Auguri ad Albert Einstein e a Sasha Grey
Il 14 marzo è anche il compleanno di Einstein, che è nato in questo giorno del 1879 a Ulm. Einstein visse a Princeton, New Jersey, per oltre vent’anni, mentre lavorava all’Istitute for Advanced Study. La città di Princeton festeggia la doppia ricorrenza con una serie di iniziative tra cui la gara di mangiatori di torte (PIe rotonde, che hanno il Pi greco dentro) e il contest dei sosia/cosplayer di Albert Einstein.
Ma è anche il compleanno di Michael Caine e di Sasha Grey (e, curiosamente, di altre tre porno-attrici).
11. I Viπ
Tra i tanti modi di celebrare il Pi Day, il luogo in cui è nato, l’Exploratorium di San Francisco, si distingue. Nel
programma di eventi è citata anche una marcia di Viπ (Very Important Pi): le prime 58 persone in coda all’ingresso, alle 9:26:53 (3,14159265358…) potranno avere accesso alla Pi Shrine, una lastra di ottone con incise un centinaio di cifre del Pi che si trova nella Public Plaza dell’Exploratorium. Più tardi, all’1:59, si terrà una seconda Pi Procession, con circa 500 persone che a loro volta gireranno 3,14 volte intorno alla Pi Shrine.
12. Per quelli che arrotondano
Se il Pi Day, con le sue evocazioni di infiniti decimali vi fa venire le vertigini, un giorno migliore per voi potrebbe essere il 22 luglio, ossia il Pi Approximation Day, dal fatto che la frazione 22/7 è una comune approssimazione per eccesso di Pi greco.
13. Il Pilish e la Cadaeic Cadenza
Nel 1996, Mike Keith, un matematico americano, realizzò un brillante esempio di scrittura vincolata, quel genere letterario in cui i testi sono stesi rispettando stabilite restrizioni. Nel caso di Cadaeic Cadenza il vincolo era che il numero di lettere di ogni parola seguisse le prime 3835 cifre del Pi Greco. Questo stile di scrittura vincolata, nello specifico, è chiamato pilish.
Per esempio, l’inizio del racconto breve è:
One (3) A (1) Poem (4) A (1) Raven (5) Midnights (9) so (2) dreary (6) tired (5) and (3) weary (5)
Non solo. Lo stesso titolo “Cadaeic”, se si assegna a ogni lettera un numero che corrisponde alla sua posizione nell’alfabeto (a=1, b=2, c=3, etc.), rappresenta “3141593”, ossia il Pi greco approssimato alla sesta cifra decimale.
14. L’Indiana Pi Bill
Nel 1897, lo stato dell’Indiana tentò di fissare per legge il valore di Pi greco a 3,2. Più precisamente, il progetto di legge 246 del 1897, passato alla storia come Indiana Pi Bill, tentava di far ratificare un metodo per la quadratura del cerchio escogitato dal matematico e fisico dilettante Edward J. Goodwin, che aveva tra le sue assurde implicazioni quella di fissare il valore di Pi greco a 3,2. Proposto dal deputato dell’Indiana Taylor I. Record, il progetto non divenne mai legge grazie all’intervento, casuale, del matematico della Purdue University Clarence Abiathar Waldo. Quadrare il cerchio usando riga e compasso è impossibile (fu dimostrato rigorosamente da Ferdinand von Lindemann nel 1882) ed è una condizione strettamente legata alla trascendenza di Pi greco.
14+1. Il tuo numero preferito è dentro Pi greco?
Avete un numero preferito? Molto probabilmente compare all’interno delle cifre decimali di Pi greco. Andando qui è possibile inserire il vostro numero preferito (oppure, per esempio, la vostra data di nascita) e scoprire dov’è localizzato nelle prime cento milione di cifre decimali di Pi greco. La probabilità di trovarlo va dal 100 per cento (se il numero ha fino a cinque cifre), allo 0,09995 per cento se è composto da 11 cifre.
14+2. La salute di un computer 
“Calcolare le cifre di Pi greco è lo stress test finale per un computer – una sorta di cardiogramma digitale” (Ivars Peterson, Islans of Truth)
14+3. Larry Shaw
Ora in pensione, è anche conosciuto come Prince of Pi.
FONTE

2.194